概率图模型：HMM和CRF

[TOC]

概述

结构化学习(Structured Learning)

概率图模型属于结构化学习的一种，把$F(x,y)$换成了概率。

结构化学习中有三个问题：

概率图模型(Graphical Model)

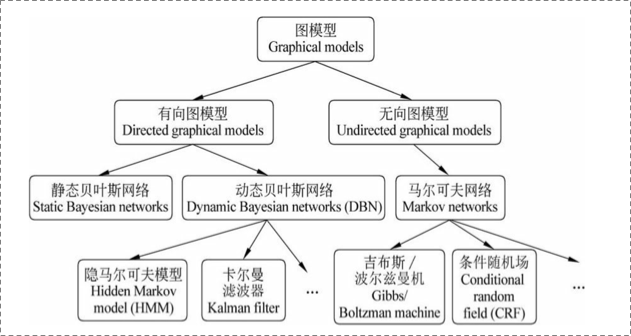
隐马尔科夫模型(Hidden Markov Model)

简介

【定义】

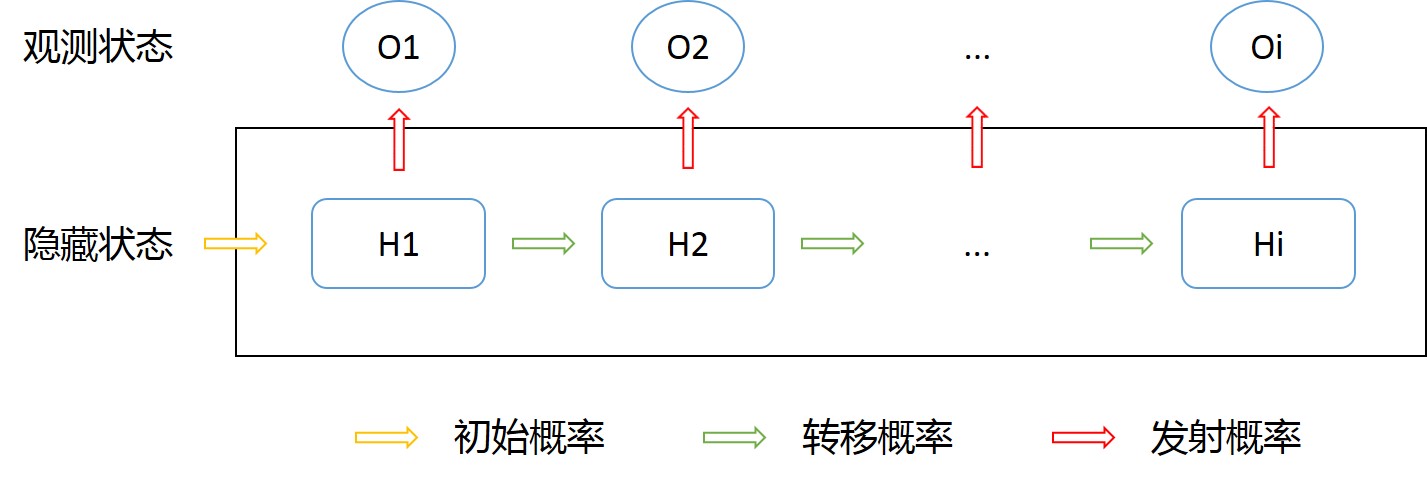
HMM(Hidden Markov Model)是一个概率模型，用来描述一个系统隐藏状态的转移概率和观测状态（隐藏状态的表现）的发射概率。
HMM是关于时序的概率模型,描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列,再由各个状态生成观测随机序列的过程.
- Hidden：说明状态的不可见性，即隐藏状态。
- Markov：说明状态和状态之间是Markov Chain。
  
  Markov Chain服从Markov性质——无记忆性：任一时刻的状态只依赖于前一时刻，而不受更往前时刻的状态的影响。
- 隐藏状态：指一些外界不便于观察（或观察不到）的状态。
- 观测状态：指可以观察到的，由隐藏状态产生的外在表现特点。

【五个要素】

观测状态
隐藏状态
初始概率
转移概率
发射概率

注：概率都可以用矩阵表示出

【三个假设】

齐次马尔可夫假设：又叫一阶马尔可夫假设，即任意时刻的状态只依赖前一时刻的状态，与其他时刻无关。
观测独立性假设：任意时刻的观测只依赖于该时刻的状态，与其他状态无关。
参数不变性假设：五个要素不随时间的变化而改变，即在整个训练过程中一直保持不变。

【三个问题】

Scoring（概率计算问题）
- 问题描述：在已知模型参数和观测序列的条件下，求给定观测序列出现的概率。即得到概率公式。
- 解决算法
  - 暴力算法：O($T*N^T$)
    
    I的遍历个数为$N^T$，加和符号中有$2^T$,T是观测状态的数目
  - 前向算法：O($T*N^2$)
  - 后向算法：O($T*N^2$)
Matching(Decoding)：
- 问题描述：已知模型参数和观测序列，求观测序列对应的最可能的状态序列。即计算概率最大的状态序列。
- 解决算法
  - 近似算法$\to$贪心思想$\to$局部最优
    
    此算法思想是在观测O的前提下每个时刻t选择该时刻概率最大的状态。
  - 维特比算法$\to$动态规划
Training：Baum-Welch算法
- 问题描述：已知观测序列，估计模型参数。
- 解决算法
  - 监督学习算法
  - 非监督学习算法：Baum-Welch算法(EM)算法

【资料】

隐马尔可夫模型（HMM）原理

原理

三个基本问题求解算法

概率计算问题

第一行是隐藏状态序列
第二行是观测状态序列

前向算法

【定义】

给定隐马尔科夫模型$\lambda$,当第t个时刻的状态为i时，前面的时刻分别观测到$y_1,y_2,…,y_t$的概率称为前向概率。 $\alpha_t(i)=P(y_1,y_2,…,y_t,q_t=i|\lambda)$。

【输入输出】

输入：隐马尔科夫模型$\lambda$，观测序列$Y$
输出：观测序列概率$p(Y|\lambda)$

【步骤】

初值
$\alpha_1(i)=\pi_i b_{iy_1}\qquad i=1,2,...,N$
其中，$\pi$是初始状态概率向量，$b_{iy_1}$是观测概率矩阵（即发射概率矩阵）$B$的对应第i个隐藏状态观测到观测状态$y_1$的概率。
递推

注：t+1时刻的前向概率$\alpha_{t+1}(i)$的求法是：所有t时刻的隐藏状态转移到t+1时刻的隐藏状态的概率之和与t时刻的发射概率的乘积。

解：
- t时刻的状态为j的前向概率是$\alphat(j)$，现在时刻t状态为j的概率已知，乘上状态j转移到状态i的转移概率就是t+1时刻的状态为i的概率，即$\alpha_t(j)a{ji}$
- 由状态到观测，乘上状态i得到观测$y{t+1}$的概率$b{iy_{t+1}}$
最终

注：
- 如果令前向概率中的t=T,即$\alpha_i(T)=P(y_1,y_2,…,y_T,q_T=i|\lambda)$，即最后一个时刻位于第i个状态时，观测到$y_1,y_2,…,y_T$的概率，即$P(Y,I|\lambda)$
- 因此，如果对$\alphaT(i)$的i求和，即$\alpha_T(1)+\alpha_T(2)+…+\alpha_T(N)$，则是观测序列的概率$P(Y|\lambda)$，因此则可以求得观测序列的概率$P(Y|\lambda)=\sum{i=1}^T\alpha_T(i)=\alpha_T(1)+\alpha_T(2)+…+\alpha_T(N)$

后向算法

【定义】

给定隐马尔科夫模型$\lambda$,当第t个时刻的状态为i时，后面的时刻分别观测到$y{t+1},y{t+2},…,yT$的概率称为后向概率。 $\beta_t(i)=P(y{t+1},y_{t+2},…,y_T|q_t=i,\lambda)$。

【输入输出】

输入：隐马尔科夫模型$\lambda$，观测序列$Y$
输出：观测序列概率$p(Y|\lambda)$

【步骤】

初值
$\beta_T(i)=1$
注：因为T时刻之后已经没有任何时刻，不需要观测任何序列，因此概率为1.
递推
$对于t=T-1,T-2,...,1\\ \beta_t(i)=\sum_{j=1}^N(a_{ij} {b_{jy_{t+1}}} {\beta_{t+1}(j)})$
注：根据t+1时刻的后向概率计算t时刻的后向概率$\beta_t(i)$。

$\betat(i)$=$\sum$(第t时刻位于第i个状态转移到第t+1时刻位于第j个状态的概率$a{ij}$ 第t+1个时刻第j个状态的发射概率$bjy{t+1}$ 第t+1个时刻的后向概率)
最终
$P(Y|\lambda)=\sum_{i=1}^N{\pi_i}{b_iy_1}\beta_1(i)$

前向后向概率的关系

拥有所有观测时，第t时刻第i个状态的概率=t时刻的前向概率*t时刻的后向概率,即

预测问题(解码问题)

Viterbi算法

【思想】

先从前向后推出一步步路径的最大可能，最终会得到一个从起点连接每一个终点的m条路径（假设有m个终点）
确定终点之后反过来选择前面的路径
确定最优路径

简言之：

每个子部分只存储最优子路径，而不是暴力枚举所有路径来获得最优路径。

从开始状态之后每走一步，就记录下到达改状态的所有路径的概率的最大值。
然后以此最大值为基准继续向后推进。

【输入输出】

输入：模型$\lambda=(A,B,\pi)$和观测$O=(o_1,o_2,…,o_T)$

输出：最优路径$I^=(i_1^,i_2^,…,i_T^)$

【定义】

变量$\delta_t(i)$：在时刻t状态为i的所有路径中概率的最大值。

由定义可得变量$\delta$的递推公式
$\delta_{t+1}(i)=\max_{i_1,i_2,...,i_t}P(i_{t+1}=i,i_t,...,i_1,o_{t+1},...,o_1|\lambda)\\ =\max_{1\leq j \leq N}[\delta_t(j)a_{ji}]b_i(o_{t+1}), \qquad i=1,2,...,N;t=1,2,...,T-1$

变量$\psit(i)$：在时刻t状态为i的所有单个路径$(i_1,i_2,…,i{t-1},i)$中概率最大的路径的第t-1个结点。

【步骤】

初始化
递推

对$t=2,3,…,T$
终止
最优路径回溯
$对t=T-1,T-2,...,1\\ i_t^*=\psi_{t+1}(i_{t+1}^*)$

求得最优路径$I^=(i_1^,i_2^,…,i_T^)$

缺点

标注偏好(Label Bias Problem)

模型在为输入序列打标签的时候，会存在偏心问题，会倾向于选择某些标签，导致最终的序列并不是概率最大的序列。

【原因】

HMM的状态转移概率的计算方式对于每一步的状态转移都会进行归一化。

CRF对其改进，在全局进行归一化：

应用

POS Tagging

根据观察到的句子x，找到隐藏的词性序列$y$，即找到最大概率的词性序列$\hat{y}=argmaxP(x,y)$

通过穷举的方式找到最大序列并不现实，因此选用Viterbi算法。

条件随机场

简介

条件：指条件概率。

随机场：
- 随机场包含两个要素：位置和相空间。当给每一个位置中按照某种分布随机赋予相空间的一个值之后，其全体就叫做随机场。
- 由若干个位置组成的整体，当给每一个位置中按照某种分布随机赋予一个值之后，其全体就叫做随机场。
  
  举词性标注的例子：假如有一个十个词形成的句子需要做词性标注。这十个词每个词的词性可以在已知的词性集合（名词，动词…)中去选择。当我们为每个词选择完词性后，这就形成了一个随机场。
马尔科夫随机场：马尔科夫随机场是随机场的特例，它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关，和与其不相邻的位置的赋值无关。

举词性标注的例子：如果我们假设所有词的词性只和它相邻的词的词性有关时，这个随机场就特化成一个马尔科夫随机场。比如第三个词的词性除了与自己本身的位置有关外，只与第二个词和第四个词的词性有关。

【三个问题】

概率计算问题：前向-后向算法
学习问题：
- 梯度下降法
- 拟牛顿法（BFGS算法）
预测问题（解码问题）：Viterbi算法

原理

【表示形式】

普通形式
向量内积形式

其中，$Z(x)$是归一化因子。

三个基本问题求解算法

计算概率问题：前向-后向算法

学习问题

预测问题（解码问题）：Viterbi算法

预测问题就是从多个候选标注中挑选出来一种标注概率最高的。由于归一化因子不影响值的比较，所以只需要比较分子部分的『非规范化概率』。

【定义】

变量$\delta_i(l)$：到位置i的各个标记$l=1,2,…,m$的非规范化概率的最大值。

$\delta_i(l)=\max_{1 \leq j \leq m}\{\delta_{i-1}(j)+w \bullet F_i(y_{i-1}=j,y_i=l,x) \}, \qquad l=1,2,...,m$

变量$\psi_i(l)$：非规范化概率最大值的路径

$\psi _i(l)=arg \max_{1 \leq j \leq m} \{ \delta_{i-1}+w \bullet F_i(y_{i-1}=j,y_i=l,x)\}, l=1,2,...,m$

【输入输出】

输入：特征向量F(y,x)和权值向量w,观测序列$x=(x_1,x_2,…,x_n)$

输出：最优路径$y^=(y_1^,y_2^,…,y_n^)$

【步骤】

初始化
$\delta_1(j)=w \bullet F_1(y_0=start,y_1=j,x), \qquad j=1,2,...,m$
注：求出各位置1的各个标记j=1,2,…,m的非规范化概率
递推

注：
- $\delta_i(l)$：到位置i的各个标记$l=1,2,…,m$的非规范化概率的最大值
- $\psi_i(l)$：非规范化概率最大值的路径
终止

注：
- 直到i=n时终止，求得非规范化概率的最大值为$\maxy(w \bullet F(y,x))=\max{1\leq j \leq m}\delta_n(j) $
- 最优路径的终点：$yn^*=arg \max{i \leq j \leq m} \delta_n(j)$
返回路径
$y_i^*=\psi_{i+1}(y_{i+1}^*), \qquad i=n-1,n-2,...,1 \\ 求得最优路径y^*=(y_1^*,y_2^*,...,y_n^*)$

其中

$w=(w1,w2,...,w_k)^T \\ F(y,x)=(f_1(y,x),f_2(y,x),...,f_K(y,x))^T\\ f_k(y,x)=\sum_{i=1}^n f_k(y_{i-1},y_i,x,i), \qquad k=1,2,...,K$

关系演变

优点

CRF是对序列建模，模型假设考虑了标签之间的依赖关系（转移特征），最终输出的条件概率是某条序列的条件概率。
- 采用分类器的方法，建模时没有考虑标签之间的依赖关系，模型训练时的目标函数也是为了提高分类准确率。
CRF着眼于局部最优解

线性链条件随机场

处理流程

对输入序列的每一个token，根据当前token和前一个token的特征计算状态函数得分和转移函数得分之和，这一步会产生多种可能的路径，每一步会得到一个矩阵
重复步骤1直到序列结束
利用维特比算法求得最优序列

原理

【特征函数】

特征函数接受四个参数：

s：表示一个句子
i：表示句子s中的第i个单词
l_i：表示给第i个单词标注的词性
l_{i-1}：表示给第i-1个单词标注的词性

输出值是0或1。

0表示要评分的标注序列不符合这个特征。
1表示要评分的标注序列符合这个特征。

【概率】

定义好一组特征函数后，给每个特征函数$f_j$赋予一个权重$\lambda_j$。

只要有一个句子$s$，一个标注序列$l$，则可以利用定义的特征函数集对$l$评分。

$score(l|s)=\sum_{j=1}^m \sum_{i=1}^n \lambda_j f_j(s,i,l_i,l_{i-1})$

上式中有两个求和，外面的求和用来求每一个特征函数$f_j$评分值的和，里面的求和用来求句子中每个位置的单词的特征值的和。

对这个分数进行指数化和归一化，则可以得到标注序列$l$的概率值$p(l|s)$

区别

HMM：生成式模型。CRF：判别式模型。
HMM：概率有向图。CRF：概率无向图。
HMM：局部最优。CRF：全局最优。
HMM：导致label bias问题。CRF：概率归一化合理。